2. Optimizer
: 손실함수의 값을 최소화하는 하이퍼 파라미터의 값을 찾는 것(하이퍼 파라미터: 사람이 파라미터 값을 조절할 수 있는 것들, ex:batch-size, learning-rate…)
어떤 optimizer를 사용하느냐에 따라 손실함수를 줄여나가며 학습하는 방법이 달라진다.
-
신경망 학습의 목적 : 손실함수의 값을 가능한 한 낮추는 매개변수 찾기=>매개변수의 최적값을 찾는 문제 => 이것을 최적화라고 한다.
-
-
2.1. 경사 하강법 (Gradient Descent)
-
경사를 따라 내려가며 가중치 업데이트
-
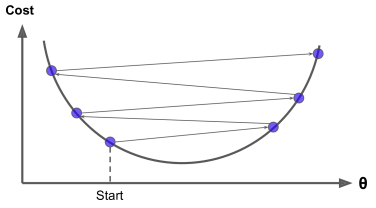
학습률이 너무 크면 학습시간이 짧아지지만 전역 최솟값에서 멀어질 수 있다.
-
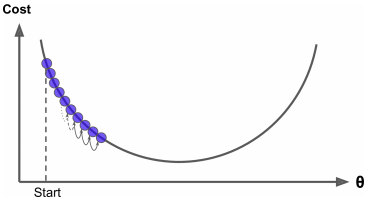
학습률이 너무 작으면 학습시간이 오래걸리고 지역 최솟값에 수렴할 수 있다.
-
학습률 너무 클때 :최소점에 수렴하지 못하고 지그재그로 이동
-
학습률 너무 작을 때 :매번 스텝마다 매우 작게 움직여 파라미터 최적화되기 오랜시간 소요
-
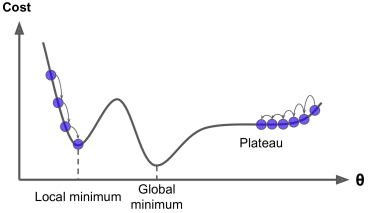
문제점 : 지역 극솟값에 머무르게 되어 학습이 정체되는 현상이 발생할 수 있음–> 모멘텀 기반 방식으로 해결한다.
-
-
2.2. 배치 경사 하강법(Batch Gradient Descent)
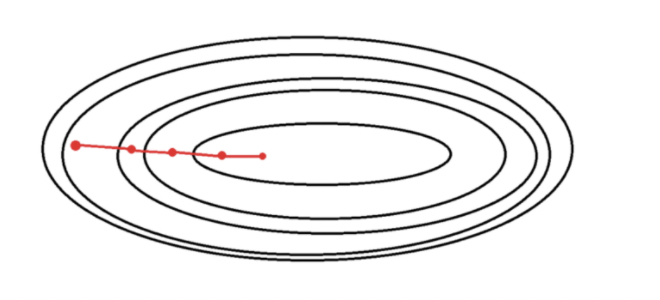
- 한번 비용함수의 기울기를 계산할 때 마다 모든 샘플을 사용하는 것=전체 학습 데이터를 하나의 배치로 묶어 학습시키는 경사하강법
- 전체 데이터를 통해 학습시키기 때문에 가장 업데이트 횟수가 적다 (1 epoch당 1회 업데이트)
-
배치(batch) : 모델의 가중치를 한번 업데이트시킬 때 사용되는 샘플들의 묶음
-
배치를 전체 데이터로 두는 것
-
장점 :
- 전체 데이터에 대해 gradient를 계산해서 진행하기 때문에 최적으로의 수렴이 안정적으로 진행된다.
- 전역 최솟값을 찾을 수 있다.
- 전체 데이터에 대해 gradient를 계산해서 진행하기 때문에 최적으로의 수렴이 안정적으로 진행된다.
-
단점:
- 한 스텝에 모든 학습 데이터를 사용해서 학습이 오래걸린다.
- 지역 최적화 상태가 되면 빠져나오기 힘들다.
- 모델 파라미터의 업데이트가 이루어지기 전까지 모든 학습데이터에 대해 저장해야하기 때문에 메모리가 많이 필요하다.
- 한 스텝에 모든 학습 데이터를 사용해서 학습이 오래걸린다.
-
-
-
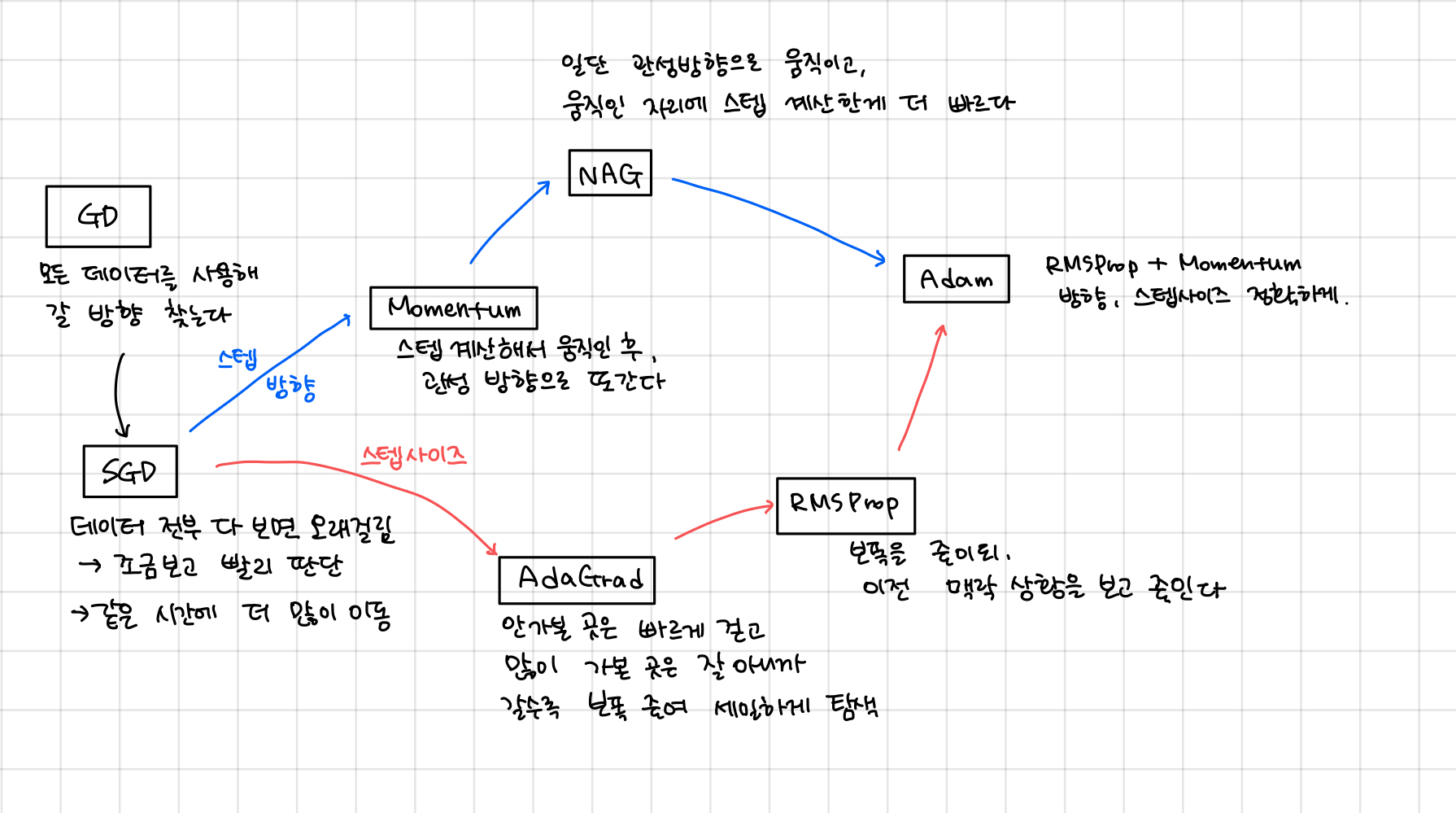
2.3. 확률적 경사 하강법(Stochastic Gradient Descent)
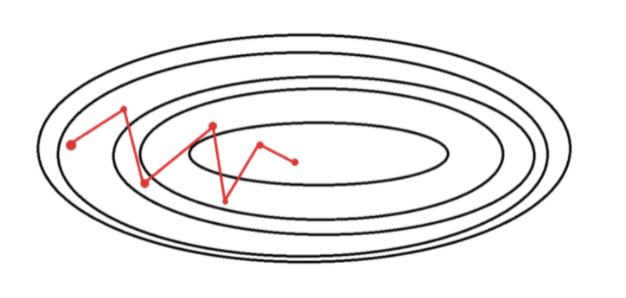
-
매 스텝에서 랜덤하게 하나의 데이터(샘플)을 선택해 GD를 계산하는 방식 (배치 크기가 1)
- 단점 : 배치 경사하강법에 비해 불안정하게 최적값으로 수렴
- 장점:
- 배치 경사 하강법에 비해 적은 데이터로 학습가능, 속도가 빠르다
- 시간과 사용되는 램 용량은 단축 가능
-
불안정 수렴을 하는 경우 Local minimun에서 탈출할 가능성이 있지만 반대로 global minimum에는 도착하지 못할 가능성이 있다. 이를 해결하기 위해서 SGD에서는 학습률을 점진적으로 감소시키는 Learning Rate Decay 기법 사용
-
1개의 데이터마다 비용함수의 기울기는 약간씩 다르기 때문에, 각각의 데이터에 대해 미분을 수행하면 기울기의 방향이 매번 크게 바뀐다.
-
Learning Rate Decay
- 학습을 시작할 때는 학습률을 크게 설정하고 점진적으로 이를 줄여 전역 최솟값에 도달하는 방식
-
Generalization(일반화) & Learning Rate
- 모델이 처음 본 데이터에 대해 퍼포먼스가 좋게하는 것–>generalization
- train set에 무한개 데이터가 있으면 성능이 좋겠지만 불가능/학습 시간 무한함. 따라서 train set, test set의 데이터에 차이가 나고 분포도 다름.
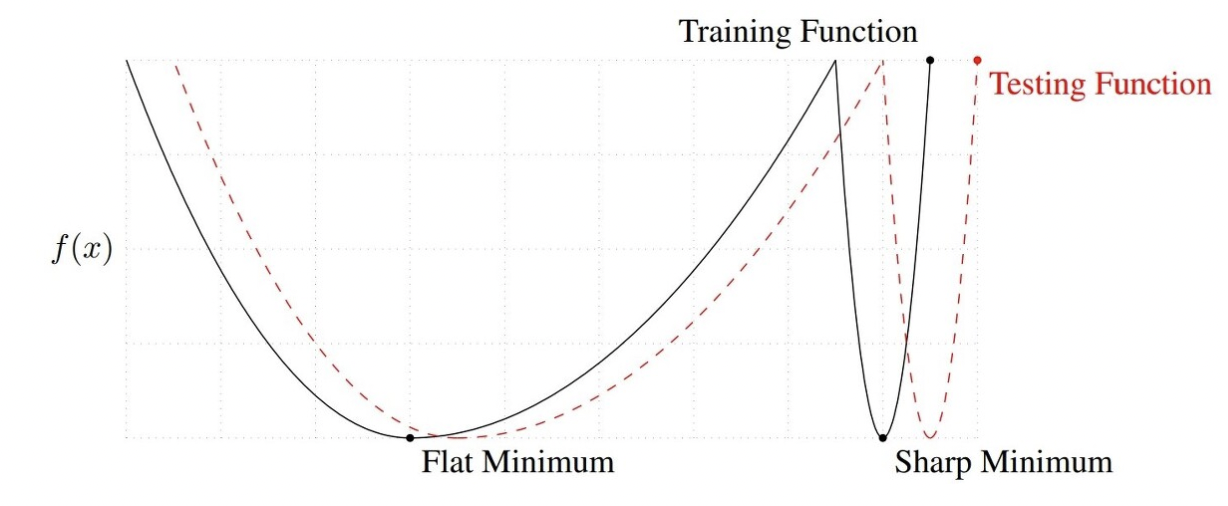
- flat이 좋은이유? training function에서 멀어져도 testing에서 성능이 크게 변하지 않기 때문
- training function과 testing function이 다른데 flat minimum이 sharp보다 안정적인 것을 볼 수 있음. 머신러닝 학습 과정에서는 손실함수를 만드는 여러개의 파라미터에 대해서 GD를 이용해 최솟값을 찾는데 generalization을 위해서는 flat minimum을 찾는게 더 좋다.
-
-
2.4. 미니 배치 경사 하강법(Mini-Batch Gradient Descent)
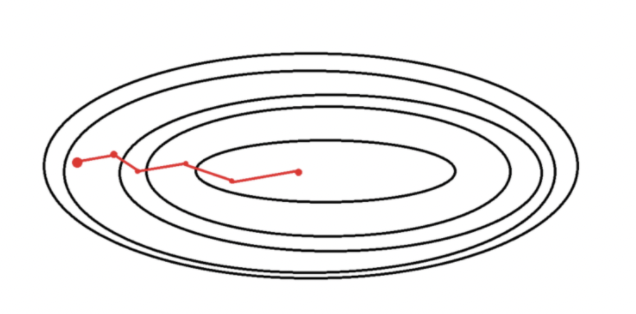
- 배치 경사하강법과 확률적 경사 하강법의 절충안, 전체 훈련세트를 1~M사이의 적절한 batch size로 나누어 학습한다.
- ex) 훈련세트가 5백만개일때 배치사이즈를 십만개라고 하면 50개 묶음이 나오므로 기울기는 1 epoch당 50번 업데이트
- 훈련세트 사이즈가 클 경우 배치 경사하강법보다 속도가 빠르다.
- shooting이 적당히 발생 (local minimum을 어느정도 피할 수 있다.)
-
2.5. AdaGrad(Adaptive Gradient)
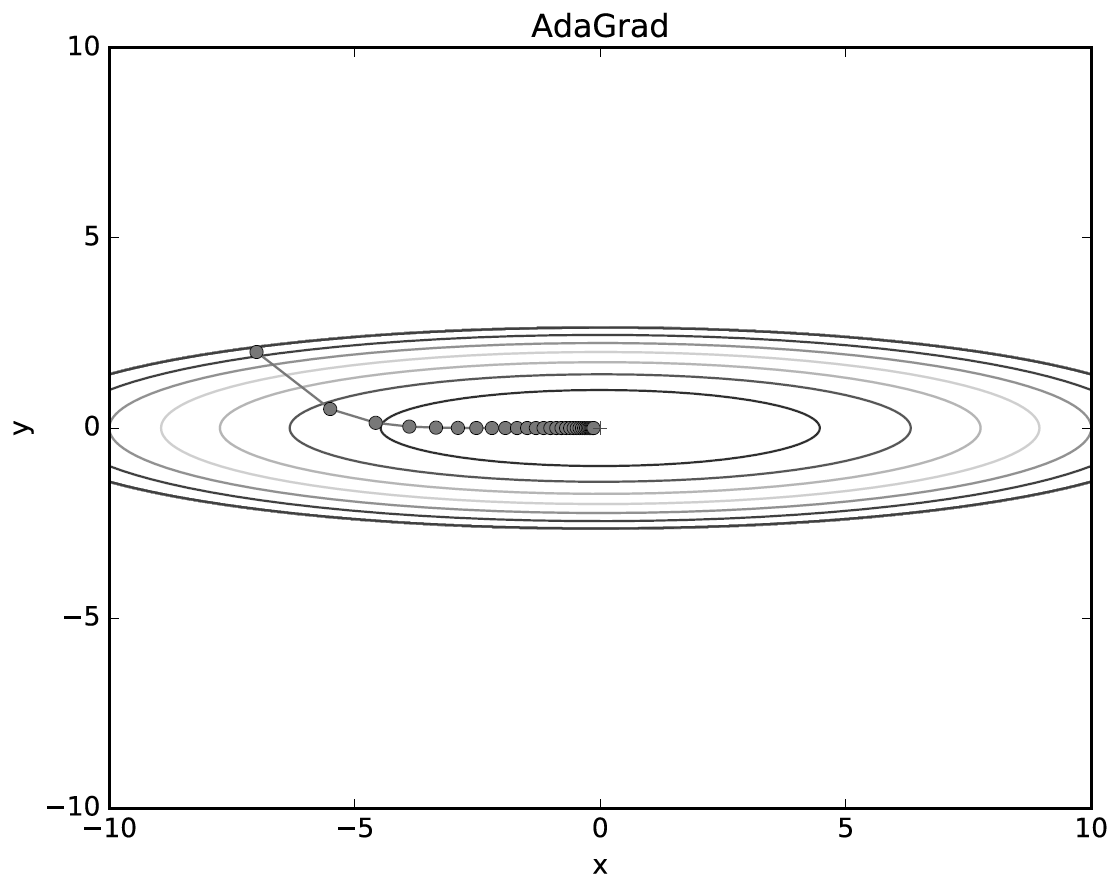
- 이때까지 파라미터가 많이 변한 파라미터는 적게 변화시키고, 적게 변화된 파라미터는 많이 변화시킴.(학습률 감소가 매개변수의 원소마다 다르게 적용됨)
- 지금까지 변화가 많았던 변수들을 optimum근처에 있을 확률이 높으므로 학습률 감소, 세밀하게 업데이트한다.
- y축 방향은 기울기가 커서 처음에는 크게 움직이지만, 큰 움직임에 비례해 갱신 정도도 큰 폭으로 작아지도록 조정된다.
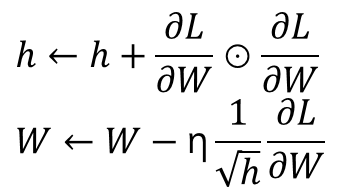
- 학습률 감소-> 학습률을 서서히 낮추는 가장 간단한 방법 : 매개변수 전체의 학습률 값을 일괄적으로 낮추는 것->여기서 발전시켜서 탄생, 각각의 매개변수에 맞춤형 값을 만들어준다.
- h: 기존 기울기의 값을 제곱하여 계속 더해준다(행렬의 원소별 곱셈)
- 매개변수 원소중 많이 움직인 원소는 학습률이 낮아진다.
- 과거의 기울기를 제곱하여 계속 더해가기 때문에 학습을 진행할수록 갱신 강도가 약해진다.
- 단점: 어느정도 시간이 지나면 학습률이 매우 작아져 업데이트가 이루어지지 않음 -> AdaDelta, RMSProp
-
2.6. RMSProp(Root Mean Square Propagation)
- AdaGrad에서는 변수가 얼마나 많이 변화했는지 Gradient 제곱의 합으로 나타내었는데 여기서는 gradient 제곱의 지수 이동 평균으로 정의한다. (지수이동평균(Exponential Moving Average)은 과거의 모든 기간을 계산대상으로 하며 최근의 데이터에 더 높은 가중치를 두는 일종의 가중이동평균법)
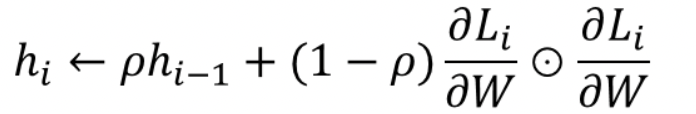
- h가 무한히 커지지 않으면서 p가 작을수록 가장 최신의 기울기를 더 크게 반영하게 된다.
-
2.7. 모멘텀 (Momentum)
- momentum: 한번 흘러간 gradient 방향을 유지시켜 준다. -> gradient가 많이 왔다갔다 해도 어느정도 학습이 잘된다.
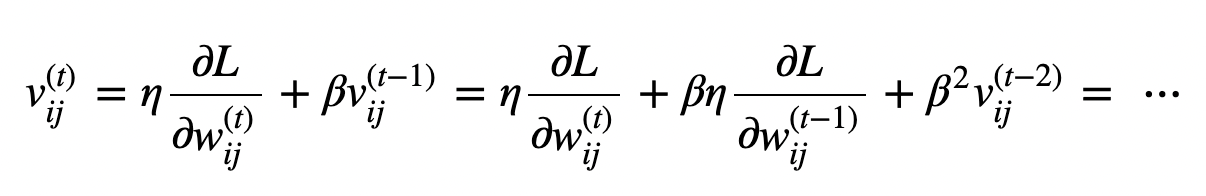
- dL/dW : W에 대한 손실함수 기울기, W: 가중치 매개변수, v: 물리에서의 속도
- 위의식: 기울기의 방향으로 힘을 받아 물체가 가속된다는 물리 법칙을 나타낸다.
- av: 물체가 아무런 힘을 받지 않을 때 서서히 하강시키는 역할.
- 베타: 0~1사이 값(보통 0.9), 이전 gradient와 현재 gradient간의 영향력 조절
- 현재 시간의 gradient에는 가장 높은 중요도, 이전 시간의 gradient에는 두번째 높은 중요도를 가지는 방식으로 이전 시간의 모든 gradient를 고려하여 방향을 설정하도록 만든다.
- SGD에 비해 지그재그 정도가 덜하다. x축의 힘은 작지만, 방향은 변하지 않아 한 방향으로 일정하게 가속하기 때문이다. y축 힘은 크지만 위아래로 번갈아 받아서 상충하여 y축 방향의 속도는 안정적이지 않다. ->전체적으로 x축 방향으로 빠르게 다가간다.
-
2.8. NAG(Nesterov Accelerated Gradient)
- Momentum은 현재 update과정에서의 기울기 값을 기반으로 미래값을 도출하도록 되어있어서 최적의 parameter를 관성에 의해 지나칠 수 있다.
- NAG에서는 momentum 계산시 이에 의해 발생하는 변화를 미리 보고 momentum을 결정한다.
- 모멘텀 방식은 현재 가속도를 고려하지 않고 속도를 설정한다면, NAG는 현재 가속도를 어느정도 고려하여 속도를 설정
- 장점: 모멘텀을 이용한 빠른 이동하면서 모멘텀에 의해 과하게 이동 가능한 점을 완화함.
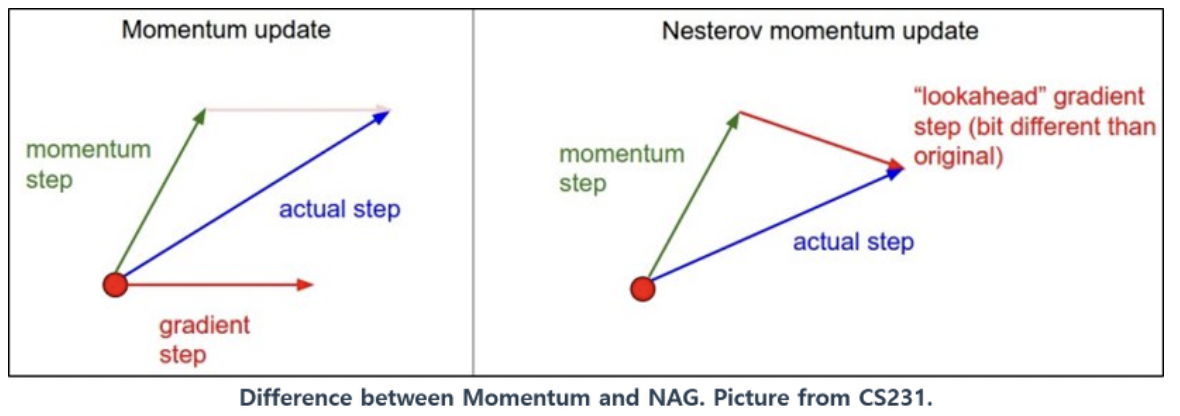
- Momentum은 현재 update과정에서의 기울기 값을 기반으로 미래값을 도출하도록 되어있어서 최적의 parameter를 관성에 의해 지나칠 수 있다.
-
2.9. 아담(Adam)
-
모멘텀(공이 그릇 바닥을 구르는듯한 움직임)+RMSProp(매개변수의 원소마다 적응적으로 갱신 정도를 조정)
-
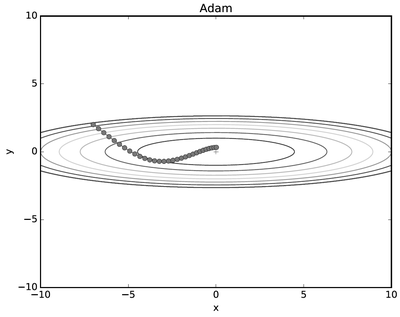
-
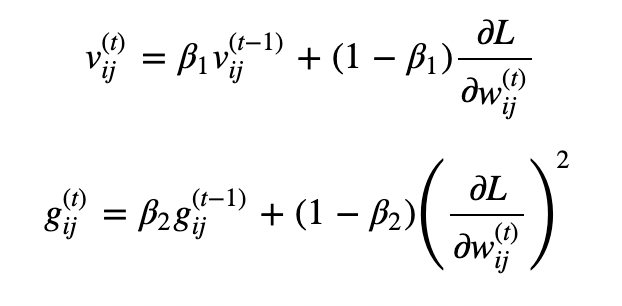

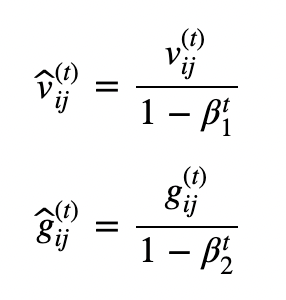
-
v, g를 그대로 이용하지 않고 unbiased expectation형태(초기에 편향된 결과로 나올수 있기 때문에 완화하기 위함)로 이용하기 위해 위의 식처럼 변형한다.
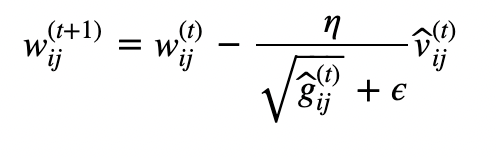
-